2 Deskriptiv dataanalyse i Jamovi
2.1 Bli kjent med Jamovi
Her finner du en video hvor Jamovi blir presentert.
I eksemplene under vil vi bruke et data sett fra Thrane (2020) som du finner her. Nå er det lurt å bruke det du lært så langt når du lagrer filene på din datamaskin. Sett opp en mappe som omhandler denne første modulen i emnet, navngi den f.eks. deskriptiv-dataanalyse og lagre filen i en undermappe som heter data. I denne mappestrukturen kan du senere lagre analysefilen fra dit statistikkprogram, eventuelle figurer og notater.
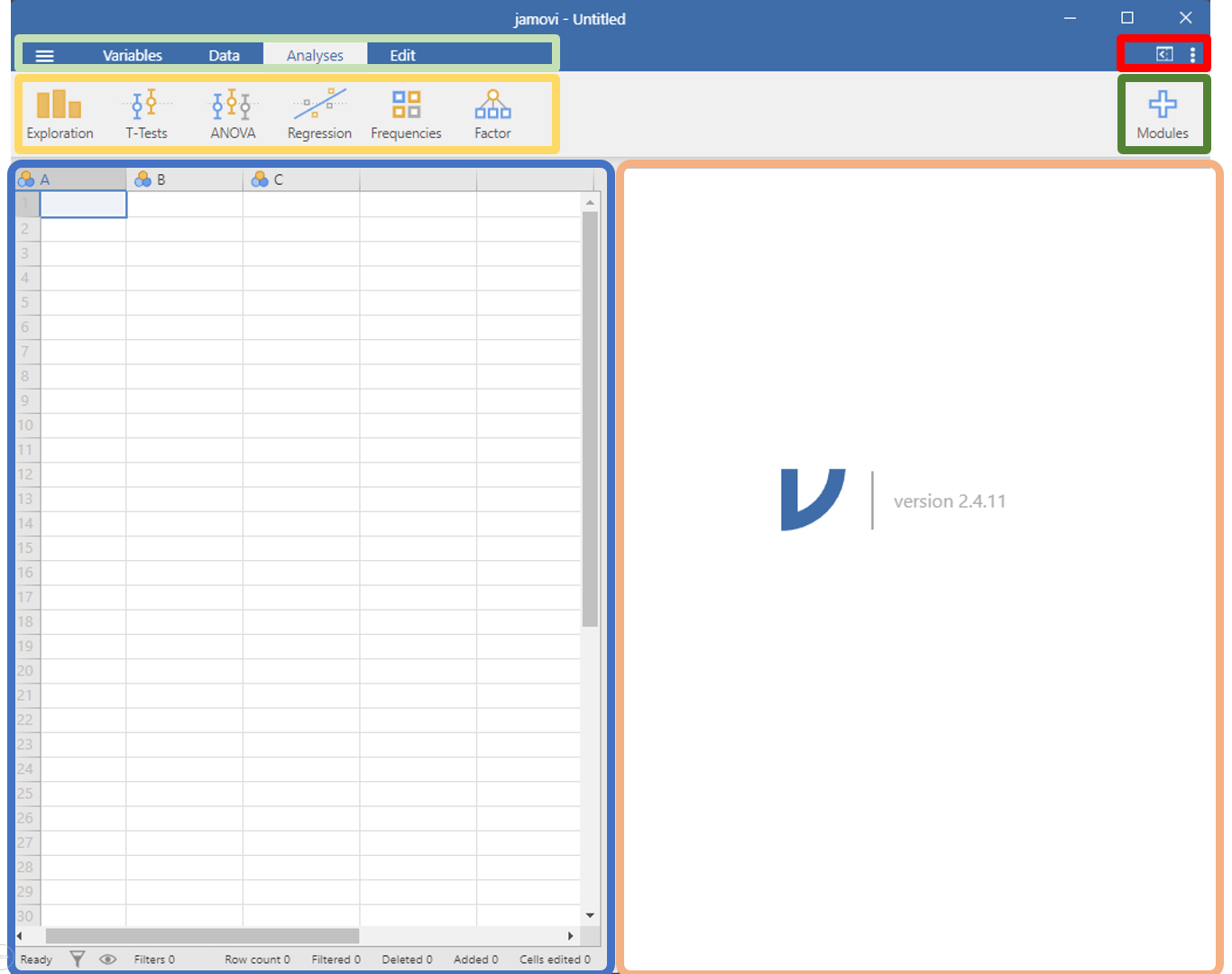
Når du har installert Jamovi og starter det for første gang vil du se følgende (Figur 2.1):
Spreadsheet: Her kan du editere data, eller se et datasett som du har importert.
Analysis output: Her vil resultater fra statistiske analyser vises. Det er også mulig å gjøre notater her koblet til hver analyse.
Modules: Her finnes muligheter å installere flere analysemoduler.
Menu: Menyen inneholder snarveier til filhåndtering, variabler, data, analyser og editering av analysefanen (Analysis output).
Analysis ribbon: De moduler for statistiske analyser som du allerede har installert finner du her.
Settings: Under innstillinger kan du forandre for eksempel fargetema på figurer og antall desimaler som skal vises i outputs.
For å importere data i Jamovi som er lagret i en csv-fil bruker vi Open i hovedmenyen. Last ned og lagre datasettet som beskrevet over og åpne det direkte i Jamovi. Bruk Browse for å finne frem til filen du ønsker å åpne. Hvis du allerede har brukt filen tidligere i Jamovi finner du den under recent (Figur 2.2). Du vil nå se datasettet representert i Jamovi i form av kolonner og rader. Legg merke til at data er strukturert som variabler i kolonner og observasjoner i rader. Navn på variabler inneholder ikke noen spesialtegn eller mellomrom, noe som kan være vanskelig for Jamovi å bearbeide. Datasettet som Thrane gir oss, er velstrukturert for videre behandling i et statistikkprogram!
Datasettet kan beskrives ytterligere i Jamovi under fanen Variables. Hvert variable er her listet med navn og du kan legge til en beskrivelse (Description) av hvert variabel. Her finnes også mulighet å editere, beregne, transformere, legge til og ta vekk variabler. Det å editere variabler innebærer at vi forandre variabeltypen.
2.2 Datavariabler
Når vi importerer et datasett prøver Jamovi å identifisere variabeltyper. I Jamovi kodes variabler som Integer (heltall), Decimal (desimaltall) eller Text (tekst, eller kombinasjon av tekst og tall).
Les mer i Jamovi User Guide
Datavariablene kodes videre som Nominal, Ordinal, Continuous eller ID. En variable på nominalnivå er en variabel som kan være en av flere mulige kategorier. Kategoriene er ikke rangerte, som for eksempel kjønn hvor en observasjon kan være mann eller kvinne. En variabel på målenivå ordinal er også kategorisk, men verdiene er rangerte. For eksempel er kategorien “høy temperatur” større enn “lav temperatur”. En variabel som beskrives som Continuous i Jamovi kan beskrives som enten intervallnivå eller forholdstallsnivå. Jamovi ønsker å vite at en variabel finnes på en skala som er kontinuerlig men skiller ikke på om variablene har et bestemt forhold mellom verdiene (forholdstallsnivå) eller hvis de bare kan beskrives med faste avstander (intervallnivå). Variabeltypen ID er lagd for å indikere grupperinger i dataene. Vi er vanligvis intressert i å analysere denne variabelen, men ønsker å gruppere datasett og analyser basert på den.
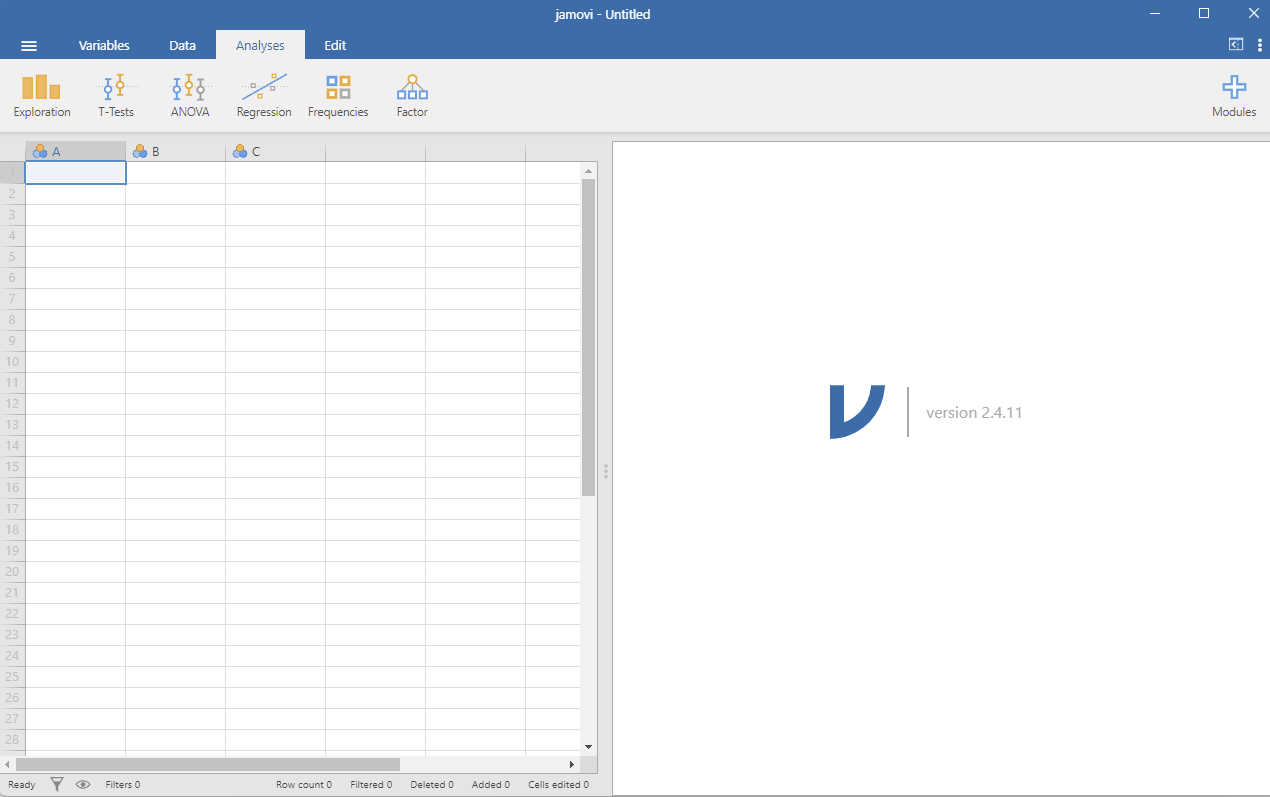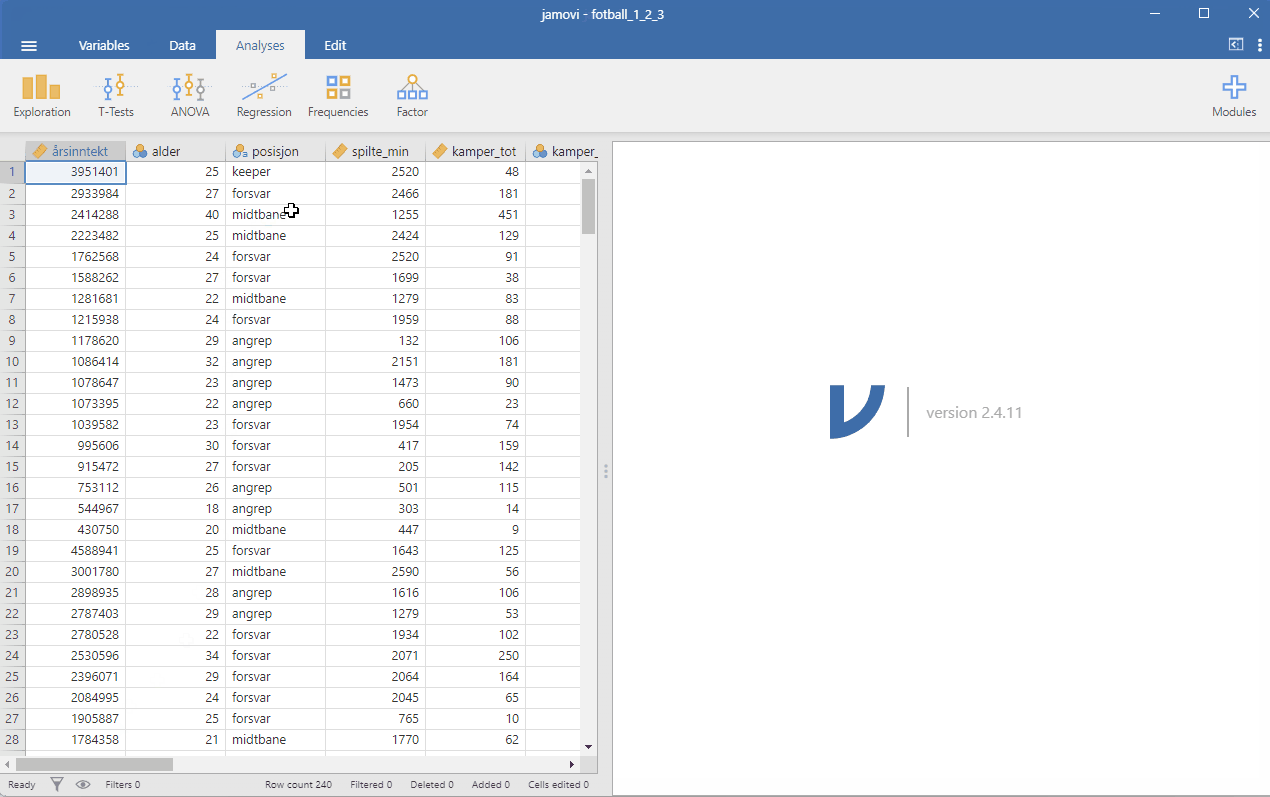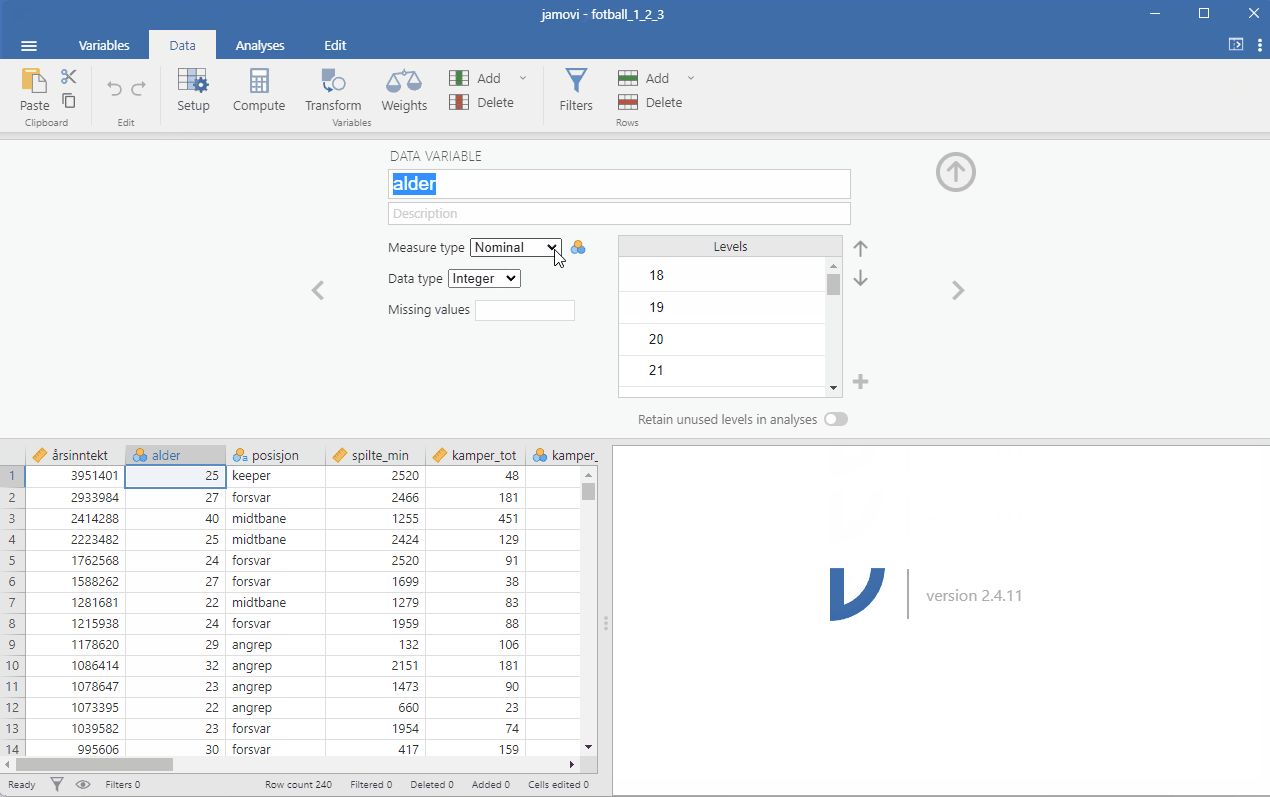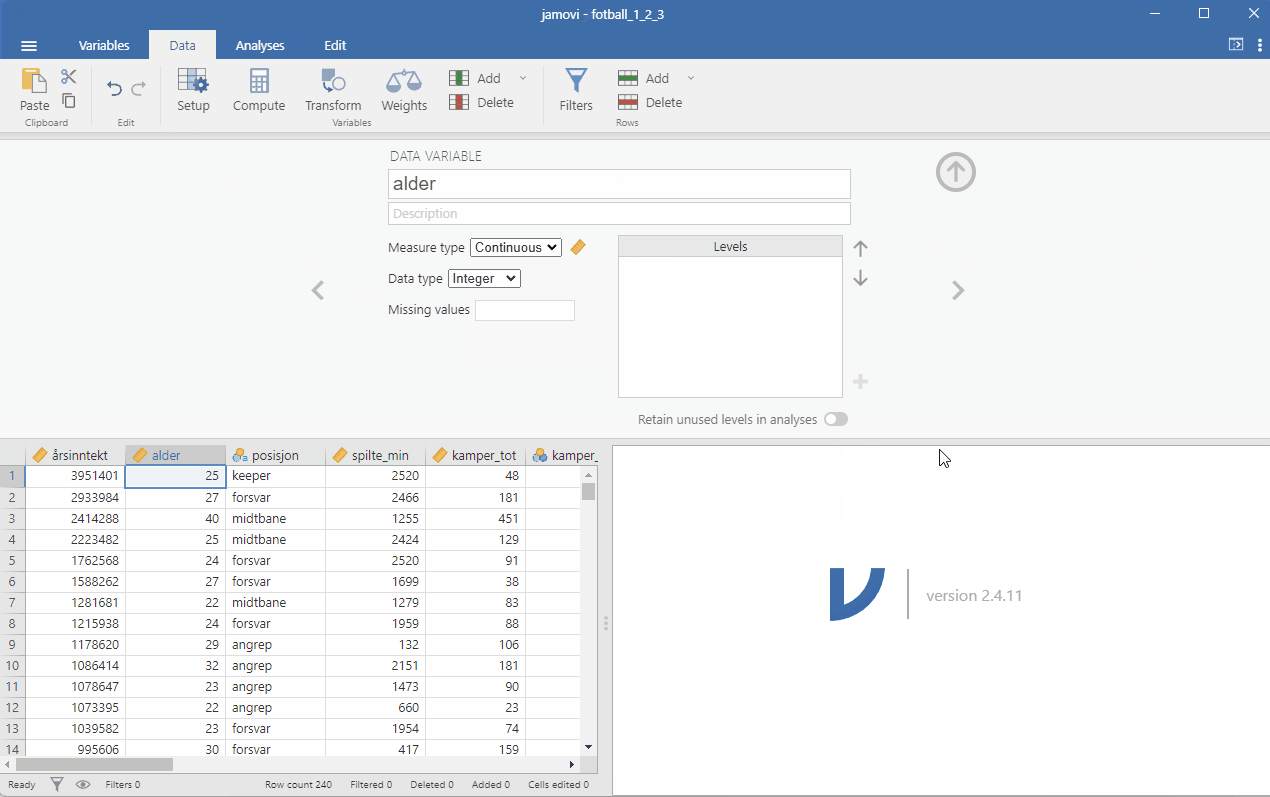
Variabler som er kodet feil kan endres til den typen som du finner er mer korrekte. Dette gjøres under fanen Data og Setup i menyen. Når du importerer filen fotball_1_2_3.csv er alder kodet som Nominal. Til tross for at variabelen ikke inneholder desimaler er koding uheldig, vi ønsker å ha variabelen alder som en kontinuerlig variabel (se Figur 2.3).
I tillegg til “rådata” kan et Jamovi-spreadsheet inneholde computed, transformed og recoded variabler. En beregnet (computed) variabel beregnes fra andre variabler og legges til datasettet ved bruk av Add funksjonen under Variables eller Data fanen. For eksempel kan vi være interesserte i å beregne spilletid per kamp. Denne ny variabelen kan beregnes som \(\frac{\text{Spilte min}}{\text{Antall kamper}}\), noe som i kode kan oversettes til =spilte_min/kamper_tot hvor spilte_min og kamper_tot er variabler i datasettet. Formelen som beregner spilletid per kamp settes inn ved å markere den nye variabelen og gå inn under Data og Setup hvor vi kan bruke formelfeltet. Her kan vi og velge fra en rekke funksjoner (under \(f_x\)) som kan brukes for å lage beregnede variabler.
Transformerte og re-kodet variabler ligner på beregnede variabler da de bruker “rådata” fra spreadsheet for å lage en ny variabel. For detaljer om transformerte og re-kodet variabler se her1.
1 Les om transformerte og re-kodet variabler i denne blog-posten.
2.3 Eksplorativ eller beskrivende analyse
Nå vi modulfanen velger Exploration åpnes en meny hvor vi kan velge Descriptives, modulen for deskriptiv statistikk. I modulen er det mulig å beregne en rekke summerende statistikker fra datasettet. I den øvre delen av modulen velger vi variabler fra listen som tilsvarer datasettet, disse flyttes inn under Variables. Hver variabel er mulig å analysere gruppert på en ordinal- eller nominalvariabel. Under Statistics velger vi hvilke statistikker vi ønsker å beregne og under Plots finnes muligheter å velge fra en rekke forskjellige typer av figurer (Figur 2.4).
Under Statistics finner vi flere valgmuligheter for å beskrive data. Sentraltendens (det typiske i dataene) kan beskrives ved hjelp av gjennomsnitt Mean, median (Median) og modus (Mode). I tillegg finner vi en funksjon for å beregne summen (Sum) for en variabel. Variasjonen (Dispersion) i dataene kan beskrives ved hjelp av standardavvik (Std. deviation), varians (Variace), variasjonsvidde (Range), minimum og maksimum (Minimum, Maximum) samt interkvartilavstand (IQR).
Beregning av variasjon som også tar hensyn til utvalgsstørrelsen finner vi under Mean Dispersion. Std. error of the mean eller standardfeilen, beregnes fra standardavvik og antall observasjoner. Når vi har flere observasjoner i utvalget er vi sikrere på estimatet av gjennomsnittet i populasjonen, noe som gjør at standardfeilen blir mindre. Denne delen grenser til det å trekke slutninger om en populasjon fra et utvalg, noe vi vil fortsette med i modul 4.
Normalitet, skweness og kurtosis er alle mål som beskriver en fordeling karakteristikk i forhold til antagelser om normalfordelte data. Noen ønsker å si noe om en variabel er normalfordelt eller ikke i forkant av analyse, det finnes noe støtte for det når vi ønsker å beskrive data ved hjelp av en sentraltendens og variasjon da en variabel som er fordelt med stor skewness vil ha et gjennomsnitt som skiller seg fra medianen. I praksis har det dog lite å si for hvordan vi analyserer en variabel. Les mer om Normality, Kurtosis og Skewness her i (Navarro and Foxcroft 2018).
Under Distribution finner vi mål som beskriver fordelingen av en kontinuerlig variabel. Ved å sammenligne variablene årsinntekt og alder i datasettet fotball_1_2_3.csv ved hjelp av Skewness og Kurtosis samt Density under Plots kan vi få et bilde av hva disse betyr. Skewness indikerer hvorvidt “halen” på en fordeling tenderer å strekke seg i noen retning. Kurtosis indikerer hvor “spiss” fordelingen er.
En fordeling, slik den du ser ved å velge Density eller Histogram under Plots, kan beskrives som normal hvis den er symmetrisk og ligner på en klokke (engelsk bell-shaped). Under Normality finnes et test for normalitet i fordelingen. Hvis Shapiro-Wilk p er lavt indikerer det at variabelen bryter med antagelse om at den er normalfordelt. Dette sammenfaller med at punktene vi ser i en Q-Q Plots ikke ligger på linjen.
Til sist kan vi bruke funksjonen for Outliers for å få en tabell over de mest ekstreme observasjonene per variabel.
Vi har allerede beskrevet noen av de figurer som er mulige å produsere under Descriptives-modulen. I tillegg til Histogram, density og Q-Q-plots kan vi lage Box-plots og Bar Plots. Hvis vi sammenligner en kontinuerlig variabel med en kategorisk (nominal eller ordinal) ser vi at en Bar Plot gir forskjellige enheter på. Under Box Plots finnes det flere muligheter for å vise data, inkludert individuelle data punkter.
De verktøy vi har snakket om så langt gir oss gode muligheter til å raskt få en overblikk over den data vi har. Figurer hjelper ofte mye mer enn numeriske sammenstillinger for å oppdage rare observasjoner, noe som kan indikere feil i dataregistrering eller koding.